【提要】 现在是 2005年末。在运用“系统易学”的基本原理成功打造3 n 阶九宫幻方系列 [2] 后,特撰写本文。在向广大易学爱好者和幻方爱好者汇报、分享成果的同时,试图探索易学九宫系统更深的机理和九宫幻方与众不同的“幻”境。
【关键词】 “系统易学” 九宫幻方 3n 阶九宫幻方 元数 元通公式 阴数模式 阳数模式
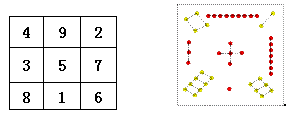
说到九宫数和幻方大多数人都不陌生,在金庸先生著名的武侠小说 《射雕英雄传》 中就有郭靖在黄 蓉的指导下为英姑指点九宫数的排列 : “戴九履一,左三右七,二四为肩,六八为足,五居中央。”这当然只是 金庸武侠 小说中的一个小插曲。事实上根据《论说》和《星子》的记载,传说在约3000年前的夏禹治水的时代有“神龟”背附神奇的星点图案出现在洛水,所以这个图案就被称为“洛书”。“洛书”上的星点图案用数字表示再引入方格图案便形成了后来的九宫格或九宫数。由于九宫数的数阵具有:“ 四正四维,皆合于十五”的特性,即三纵三横与对角三数相加之和都等于15的特殊机理,在中国古代更有“纵横图”的说法,于是也就揭开了幻方研究的序幕。 九宫数也就成为最具代表性的三三幻方,也是最早的幻方 。而 “ 四正四维,皆合于十五”也就成为判定幻方的基本要素。
易学与幻方学
由于“洛书”是幻方学的源头,同时也是传说中易学的源头之一,因此两者之间还是存在一定的同宗之缘。在中国古代对幻方的研究大都伴有易学的影子;到了近代幻方学的发展开始走向纯数学化。但同时也不断有人质疑:幻方研究来干什么用?这个看似简单的问题着实让人琢磨。在笔者看来:纯数学化的问题是一个不可回避现实问题,当然这里存在诸多的历史和现实因素,但是顺着同宗之缘的线索寻求相互支撑平台也是一种选择,毕竟我们还不完全清楚“洛书”的真正内涵。
幻方学的研究与发展到现在已颇具规模。在阶数 [3] 方面已经上千(据说还有上万的但笔者还未查到具体资料),另外还发展出了次方幻方 [4] 等幻方形式。但不论幻方学怎么发展源于“洛书”的“四正四维,皆合于十五”的神奇幻境特性始终是判定幻方的基本要素。随着“系统易学”对九宫数的进一步研究 [5] 挖掘出了九宫数更多的幻境特性“元数”、“元通公式”等,并将九宫数系统延伸到三维幻境,同时探索其内涵的原理。但这些幻境特性并不是所有幻方都能具备的;特别是我们将要看到的 3n 阶幻方系,之所以称它为幻方系就是针对九宫幻方自身所固有的与众不同的成长性而言的。因此,笔者认为有必要严谨地将以原九宫数为基础的幻方系统在幻方学中相对独立出来。笔者先称之为“九宫幻方”。此仅为个人观点。
3n 阶九宫幻方系
“系统易学”强调系统论、中心论在易学研究中的运用与作用。一方面,一个中心性的系统在对其内部具有完美和谐的中心平衡的系统有机性的同时,对外更具有无限的延伸性或成长性,延伸和成长是存在的完美表现形式;另一方面,一个成长性的系统对其原始系统不是绝对的否认,而是不断的明确与再利用。而“四正四维,皆合于十五”的特性则说明了九宫数就是一个典型的以“十”字形为中心而平衡的数阵系统。由此我们就可以得出九宫数系统是可以延伸和成长的,甚至是无限制的结论。
因此,九宫数的发展也就是对九宫数自身存在的进一步明确与再利用。即九宫数的发展要依赖以九宫数自身为要素结合自身已固有特性为保障。只有基于这样一种前提条件,并“一以贯之”地遵循才能揭示其内在的蕴涵。具体说来就是:作为三三幻方的九宫数发展的第一阶段就是九阶九宫幻方。而九宫数内在的一切特性都将遗传到九阶九宫幻方,甚至还要有所发展。而从整体上看就形成了一个 3 n 阶九宫幻方系列。
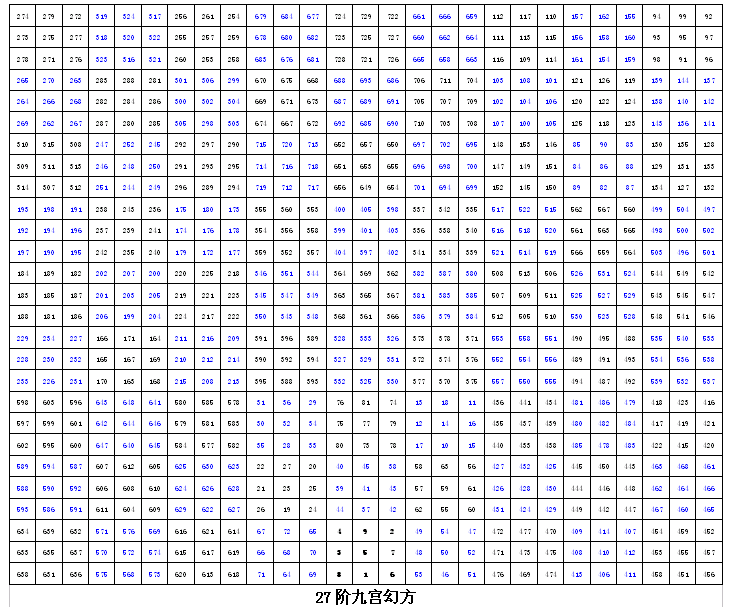
3n 阶九宫幻方系列的编排方法十分简单:任何一个3n 阶九宫幻方都有(3n ) 2 (即9 n )个数字,将这些数字按大小顺序排列并等分成9个组(而这些数字的个数则是9的倍数,也就一定能被整分成9组)。以九阶九宫幻方为例:1~9为一组,10~18为一组依此类推,将这9组数字以组内数字的大小按九宫数的分布模式排列,而其它高阶幻方的数组内的数字也以上述方法分组、排列直到一组为9个数字为止。我们可以看到:在原3阶幻方中数字“1”的位置上还可以看到完整的九宫数组合,这就是对中心性系统发展原则的一种验证。而如此排列出来的数阵 “ 四正四维,皆合于一数”完全符合幻方要求。
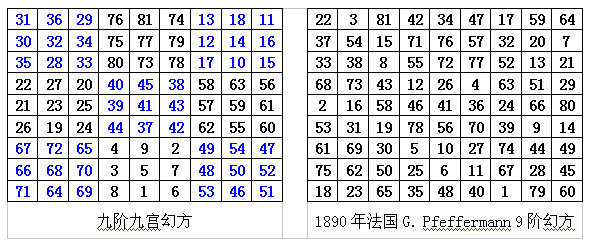
3n 阶九宫幻方系列的阶数虽然是无穷大的,但系列中幻方的基本幻境特性一致。用 1890年法国G. Pfeffermann的九阶幻方与 九阶九宫幻方进行对比。
一、 1890年法国G. Pfeffermann的九阶幻方与 九阶九宫幻方的 四正四维运算皆合于369,符合幻方要求。
二、“元数”
“元数”就是在九宫数中关于中心数“5”的相对的两个数之和总是相等的。“元数”正是形成九宫数之“四正四维,皆和于十五”的系统有机性的根本基础。“元数”体现的是关于系统中心相对着的两个要素之间的组合在系统中的一种等量平衡 [ 6] 。从“系统易学”的元数模式来看,在 1890年法国G. Pfeffermann的九阶幻方与 九阶九宫幻方中关于中心相对(对称)的2个数字之和则皆等于82。
三、普通幻方与 九宫幻方区别体现在“元通公式”
先简述一下“元通公式”。在九宫数数阵中所有的奇数都以“边联” [ 7] 关系集中在以中心数“5”为中心的周围,而所有的偶数则被分配到数阵的四个顶角,从而使九宫数数阵形成了阴数与阳数两大阵营,即构成九宫数元通公式的两种模式“阳数模式”与“阴数模式”。
(一)九宫数之元通公式阳数模式。在九宫数的阳数模式运算中不含中心数“5”。在九宫数数阵中,与中心数“5”相边联的四个阳数1、3、7、9,通过以下运算,我们可以得到如下一种一致的结论:在九宫数数阵中,除中心数“5”外,任取一个阳数A,将与阳数A关于中心相对的阳数B有边联关系的两个阴数及中心数“5”三数以一种中虚的结构一并相加之后再减去后天八卦系统的元数 “ 10”,其结果都等于阳数A。
(二)九宫数之元通公式的阴数模式。九宫数数阵中的四个阴数2、4、6、8分居在四个顶角而两两相对。通过类似阳数模式的以下运算,我们同样可以得到如下一种一致的结论:在九宫数数阵中任取一个阴数A,将与之关于中心相对的阴数B以及与阴数B有边联关系的两个阳数三数一并以一种中实的结构相加之后再减去后天八卦系统卦数的元数 “ 10”,其结果也正好等于阴数A。

四、“元通公式”在高阶九宫幻方中的计算方法
在一个3n 阶九宫幻方中,对任何一个数来说:从3阶九宫幻方到3n 阶九宫幻方形成了n种九宫关系,因此要确认一个数在3n阶九宫幻方中与那三个数的组合形成元通公式关系,就必需层层落实,从高阶向底阶依次排列。还是以九阶九宫幻方为例子;先取一个数如:“52”。52在其9阶九宫幻方和3阶九宫幻方分别居于九宫数的6数位和7数位。
第一步、根据元通公式关系模式并按高阶向底阶的顺序,确认与数“52”所在相对应的三个数的位置就应该分别在9阶幻方中3、4、9数位中。
第二步、在根据“52”在3阶九宫幻方中居于九宫数的7数位,就可以确认数“52”所在相对应的三个数的位置分别存在于9阶幻方中3、4、9数位中3阶幻方的4、5、8数位,让人惊奇的是这种跨的元通公式关系模式没有特定的位置要求。而使阶层这种元通公式关系模式的平衡面随九宫幻方的阶数不断增加而成倍增加。平衡面的增加现象体现出九宫幻方系统平衡的完美性、成长性。这一点却是普通幻方所无法做到的。
52=26+77+31-82
52=26+32+76-82
52=23+80+31-82
52=23+76+35-82
52=22+77+35-82
52=22+80+32-82
|